Razz=1.5 if a Razzberry is used, otherwise R=1.
Curve=1.7 if a Curveball is used, otherwise C=1.
Ball=2 for Ultra Balls, =1.5 for Great Balls, =1.0 for Pokéballs.
Medal = 1.3 for gold medal, =1.2 for silver medal, =1.1 for bronze medal.
Radius = the radius of the inner catch-reticle, as a fraction of the outer one.
Reticle = 1.3 if the ball landed in the inner reticle (so a bonus was achieved).
BaseCapRate is the base capture rate of that pokemon species. CpM, or "CP Multiplier", is a hidden value Niantic uses to scale stats to a particular level. It was first discovered in the GAME_MASTER file.
For dual-type pokemon, the medal bonuses are averaged. So a player with one gold, one silver type would have a bonus of M=1.25.
While the catch rate formula looks intimidating, it has a simple interpretation. The quantity inside, $$1-\frac{BaseCapRate}{2*CPM}$$ is the probability that a simple pokeball throw with no bonuses would fail. This quantity is exponentiated. If it is squared, it equals the probability that two simple pokeball throws would fail in a row. Since all of the other modifiers are in the exponent - curveball, razzberry, etc - they turn out to be equivalent to being able to throw multiple pokeballs in one turn. For example, with a curve and ultra ball, the exponent is ~3, meaning that the catch probability is equivalent to being able to throw 3 pokeballs per turn before the pokemon has a chance to escape. Lastly, subtracting the exponentiated pokeball flee rate from 1 yields the probability that the pokemon won't fail to be caught. This is the pokemon go catch formula.
Also of note: the formula never has a 0% catch chance, and can only have a 100% catch chance if the pokeball formula already had a 100% catch chance. And since the factors are multiplied, they compound: using two bonuses rather than one will disproportionately amplify their effect. And three bonuses will be dramatically better than two bonuses, etc.
On the color of the ring: While the it does correlate with catch rate, there is not a one-to-one mapping. The color of the ring is determined by the same formula, but with only the ball type in the exponent. Thus, the color is unaffected by razzberries, curve balls, medals, or reticle bonuses. This was confirmed by gakushan, who compared the RGB values of rings after the medal patch. First, a pre-0.41 data set from u/CreativiTimothy was used to find out the effect of all factors other than medals.
Each row of the data stated which factors were in play (great balls, excellent throws, etc). The data did not contain reticle size.
The formula for simple throws with great and ultra balls was already known to be the GUCT formula, but with all factors=1 except for the Ball factor "BF". The next step was to add in curve balls, since most of the ~50,000 data points were curved. The desired result was the catch probability function f(x) as a function of the inner term, 0.5*BaseCapRate/CpM, which I call x. The value of x also happens to be the catch probability function for a simple pokeball throw, or go+ attempt.
After binning the data into even intervals of dx=0.04, the catch rate within each bin was averaged to produce the bin's probability. A best fit was done to the binned data using the SciPy library in Python, and after a variety of guesses, the function which came out best was
$$f(x)=1 - (1-x) \wedge (BF*C)$$ The fit was done separately for each type of ball, and so there were different best-fit parameters C for each type. This table's columns are the corresponding best-fit exponents, their standard deviations, the guess of BF*1.7 which we used in the GUCT, the experimental/theoretical difference, and the sample size:
1.7 was not the optimal number to fit all three equations, but we chose it because the optimal number was very close to 1.7 (within error) and the game seems to use round numbers, as evidenced by the BallFactor, which was stolen from the old pokemon games' mechanics.
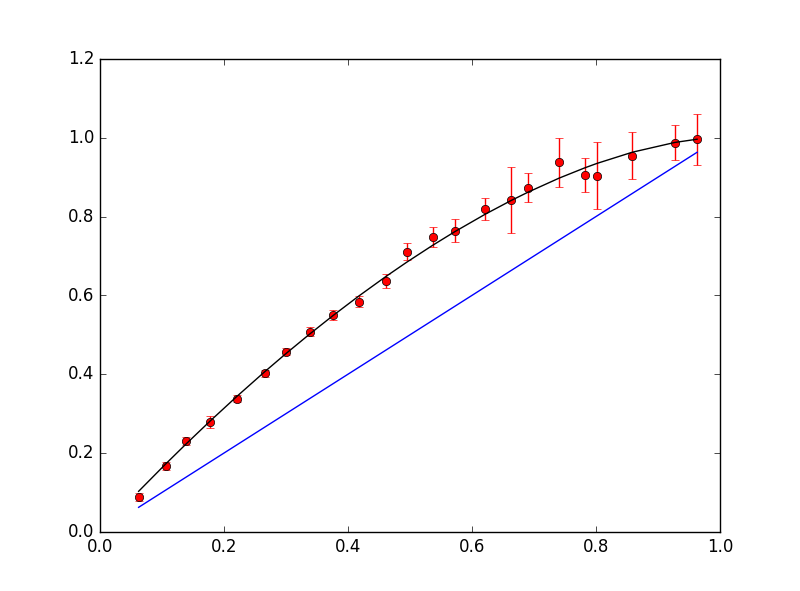
Here are the three fits for poke, great, and ultra balls, respectively. The x-axis is x=0.5*BaseCapRate/CpM and the y-axis is the probability of catching a pokemon with that x value. As Niantic fans, we chose not to include labels on our axes:
Curve=1.7 if a Curveball is used, otherwise C=1.
Ball=2 for Ultra Balls, =1.5 for Great Balls, =1.0 for Pokéballs.
Medal = 1.3 for gold medal, =1.2 for silver medal, =1.1 for bronze medal.
Radius = the radius of the inner catch-reticle, as a fraction of the outer one.
Reticle = 1.3 if the ball landed in the inner reticle (so a bonus was achieved).
BaseCapRate is the base capture rate of that pokemon species. CpM, or "CP Multiplier", is a hidden value Niantic uses to scale stats to a particular level. It was first discovered in the GAME_MASTER file.
For dual-type pokemon, the medal bonuses are averaged. So a player with one gold, one silver type would have a bonus of M=1.25.
While the catch rate formula looks intimidating, it has a simple interpretation. The quantity inside, $$1-\frac{BaseCapRate}{2*CPM}$$ is the probability that a simple pokeball throw with no bonuses would fail. This quantity is exponentiated. If it is squared, it equals the probability that two simple pokeball throws would fail in a row. Since all of the other modifiers are in the exponent - curveball, razzberry, etc - they turn out to be equivalent to being able to throw multiple pokeballs in one turn. For example, with a curve and ultra ball, the exponent is ~3, meaning that the catch probability is equivalent to being able to throw 3 pokeballs per turn before the pokemon has a chance to escape. Lastly, subtracting the exponentiated pokeball flee rate from 1 yields the probability that the pokemon won't fail to be caught. This is the pokemon go catch formula.
Also of note: the formula never has a 0% catch chance, and can only have a 100% catch chance if the pokeball formula already had a 100% catch chance. And since the factors are multiplied, they compound: using two bonuses rather than one will disproportionately amplify their effect. And three bonuses will be dramatically better than two bonuses, etc.
On the color of the ring: While the it does correlate with catch rate, there is not a one-to-one mapping. The color of the ring is determined by the same formula, but with only the ball type in the exponent. Thus, the color is unaffected by razzberries, curve balls, medals, or reticle bonuses. This was confirmed by gakushan, who compared the RGB values of rings after the medal patch. First, a pre-0.41 data set from u/CreativiTimothy was used to find out the effect of all factors other than medals.
Each row of the data stated which factors were in play (great balls, excellent throws, etc). The data did not contain reticle size.
The formula for simple throws with great and ultra balls was already known to be the GUCT formula, but with all factors=1 except for the Ball factor "BF". The next step was to add in curve balls, since most of the ~50,000 data points were curved. The desired result was the catch probability function f(x) as a function of the inner term, 0.5*BaseCapRate/CpM, which I call x. The value of x also happens to be the catch probability function for a simple pokeball throw, or go+ attempt.
After binning the data into even intervals of dx=0.04, the catch rate within each bin was averaged to produce the bin's probability. A best fit was done to the binned data using the SciPy library in Python, and after a variety of guesses, the function which came out best was
$$f(x)=1 - (1-x) \wedge (BF*C)$$ The fit was done separately for each type of ball, and so there were different best-fit parameters C for each type. This table's columns are the corresponding best-fit exponents, their standard deviations, the guess of BF*1.7 which we used in the GUCT, the experimental/theoretical difference, and the sample size:
| bestfit | stdev | BF*1.7 guess | Δ | N | |
|---|---|---|---|---|---|
| poke | 1.688 | 0.011 | 1.7 | 0.012 | 44046 |
| great | 2.605 | 0.046 | 2.55 | 0.055 | 3455 |
| ultra | 3.45 | 0.091 | 3.4 | 0.05 | 1486 |
1.7 was not the optimal number to fit all three equations, but we chose it because the optimal number was very close to 1.7 (within error) and the game seems to use round numbers, as evidenced by the BallFactor, which was stolen from the old pokemon games' mechanics.
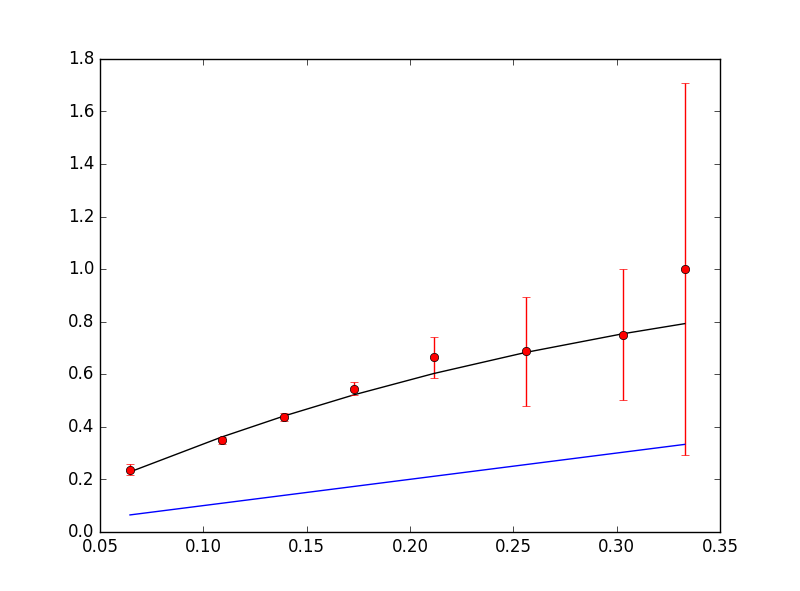
Here are the three fits for poke, great, and ultra balls, respectively. The x-axis is x=0.5*BaseCapRate/CpM and the y-axis is the probability of catching a pokemon with that x value. As Niantic fans, we chose not to include labels on our axes:
The red points are "experimental" probabilities, from the data. In particular, the red points plot the average x value of a bin against the corresponding fraction of pokemon caught in the bin. In black is the best-fit line. In blue is the probability of catching with a simple pokeball throw, for comparison. Error was due to sample size.
A small horizontal error in each red point is not pictured but exists due to the finite size of a bin, which caused a single bin to actually have slightly varying x values.
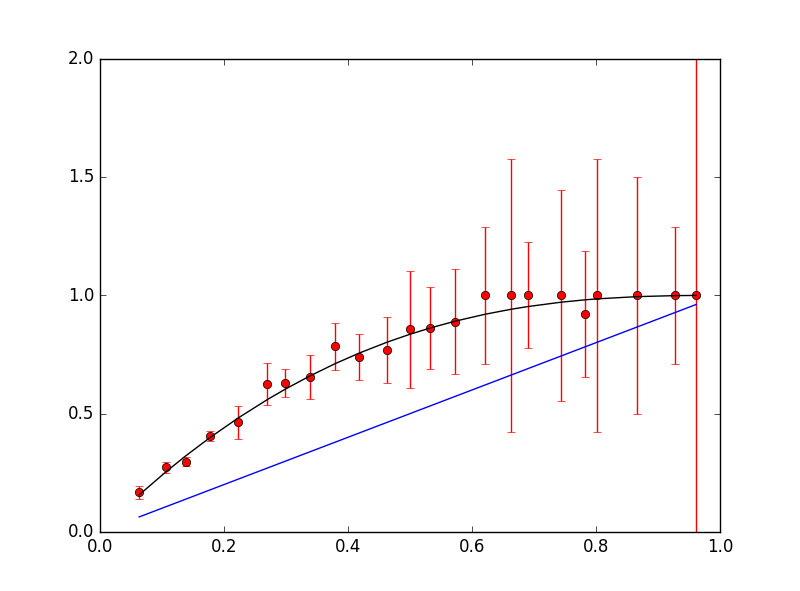
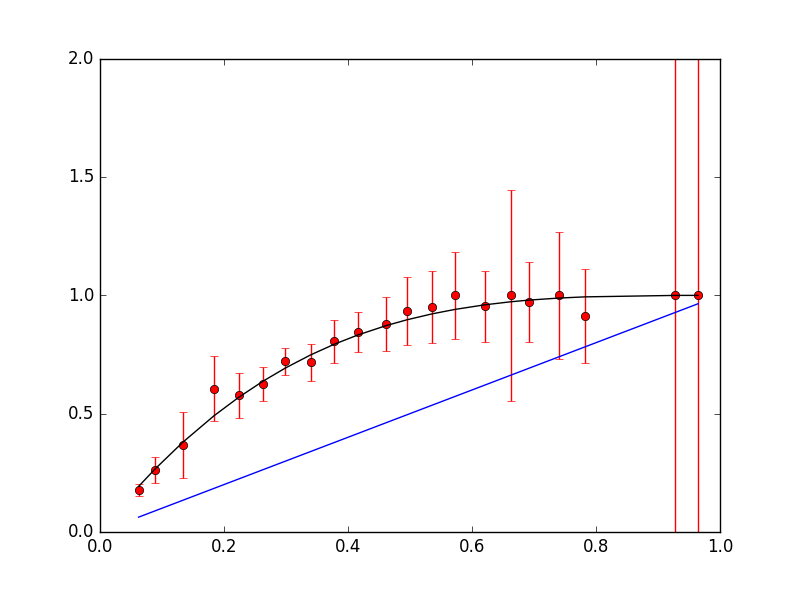
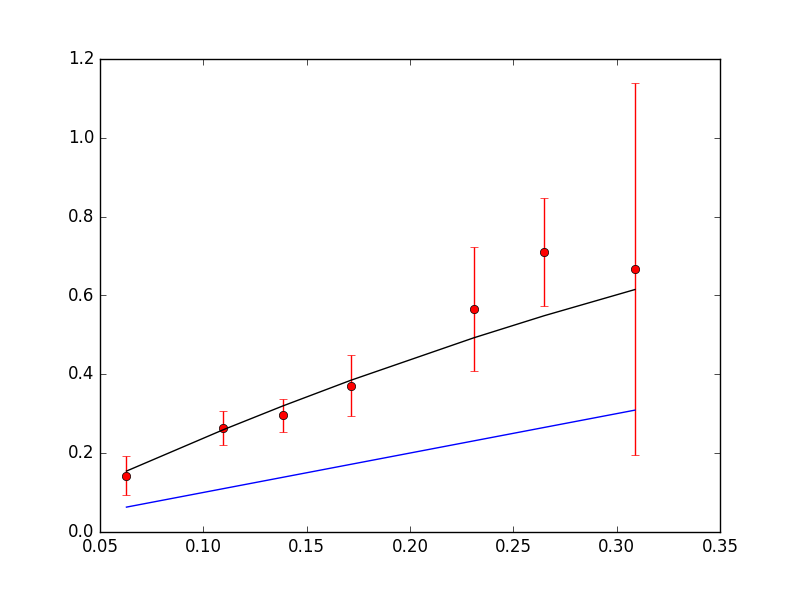
A similar procedure was used to find the berry bonus: each ball bonus was fitted separately. However, since there was very little non-curveball data, no fits were done to control for the case of razzberries without curveballs. Considering the nature of the bonuses, it is unlikely that Niantic would have made an exception for this particular case.
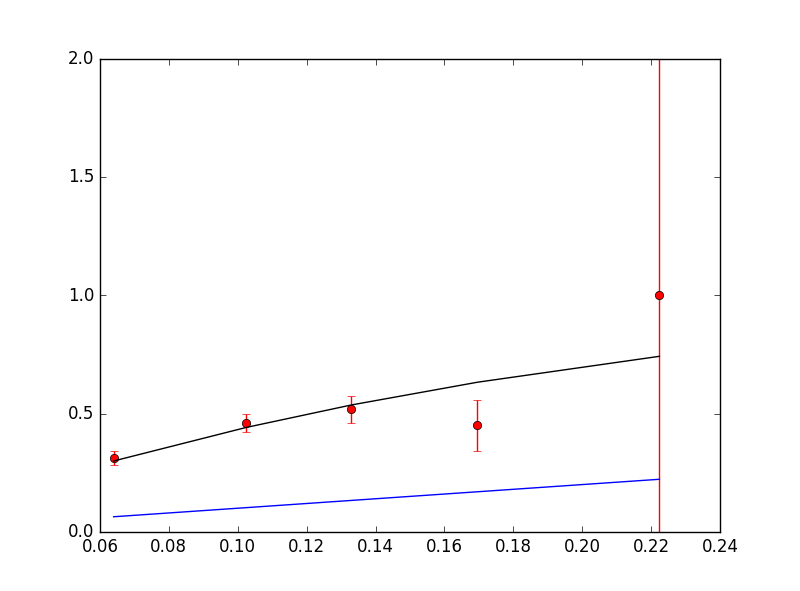
Unfortunately, another factor haunts our data: the user who created this dataset would only use a Razzberry if the catch probability was low, so there is no data for high values. There is also disproportionate use of different ball types. Below are the corresponding table and graphs for berry+curve+pokeball/greatball/ultraball:
A small horizontal error in each red point is not pictured but exists due to the finite size of a bin, which caused a single bin to actually have slightly varying x values.
A similar procedure was used to find the berry bonus: each ball bonus was fitted separately. However, since there was very little non-curveball data, no fits were done to control for the case of razzberries without curveballs. Considering the nature of the bonuses, it is unlikely that Niantic would have made an exception for this particular case.
Unfortunately, another factor haunts our data: the user who created this dataset would only use a Razzberry if the catch probability was low, so there is no data for high values. There is also disproportionate use of different ball types. Below are the corresponding table and graphs for berry+curve+pokeball/greatball/ultraball:
| bestfit | stdev | BF*C*1.5 | Δ | N | |
|---|---|---|---|---|---|
| poke | 2.583 | 0.15 | 2.55 | 0.033 | 499 |
| great | 3.884 | 0.0677 | 3.825 | 0.059 | 5795 |
| ultra | 5.391 | 0.36 | 5.1 | 0.291 | 967 |
...however, we have confidence that 1.5 is the correct Razzberry bonus for other reasons. Using MITM, we found that the server sends a line saying "RazzberryBonus = 1.5". ((((desert knows this more precisely?))))) This gives us sufficient certainty to consider 1.5 the correct number.